24時間系のジムを半年で解約した
まず初めに僕は筋トレ歴1年11ヶ月(2023/1/2現在)であり,大学のジムで主にトレーニングをしています。 そんな僕が24時間系の某ジムに半年間通って思ったことを書き並べます。24hジムってどうなの?みたいな人に刺さるかもしれません。
大学のジム
大学のジムはコスパが最強で,年会費が9000円程度で回数制限はありません(安すぎ)。開館時間は11:30-20:20であり,設備は有酸素(トレッドミル,エアロバイク),マシン,フリーウェイトなどが使用可能でそこらへんのジムより充実していると思います。あとはマナー管理が厳しく,セット間のスマホいじりや鼻出しマスクは100%注意されます。
なぜ24hジムに入会したいと思ったか
1. 休日や夜もジムに行きたい!
大学のジムは日曜,祝日は休みでGW期間や年末年始になると休館が続いてしまうのでかなり不満でした。24hジムであれば基本的に365日開きっぱなしなので,そうした制限を受けません。
現在はA.プレス系筋群(大胸筋,上腕三頭筋)の日とB.プル系筋群(背中,上腕二頭筋)+脚の日に分けており,週3回(A→B→AもしくはB→A→B)で組んでいるので同じ部位が週2回よりちょっと少ないくらいの頻度で回ることになります。そうすると疲労を厳密に管理しようと思うと中2日で組みたくなるので
月曜日A,火曜日オフ,水曜日オフ,木曜日B,金曜日オフ,土曜日オフ,日曜日A
という感じになります。しかし大学のジムは日曜や祝日が休みになるので,このスケジュールは流動的にならざるを得ません。研究が立て込んでいると開館時間に間に合わなかったりで週1回しか行けなかった,みたいなことがまあまあの頻度で起きました。
2.トレーニング動画を撮りたい!
大学のジムは盗撮等のトラブル防止のために写真・動画撮影は全て禁止です。トレーニングをしていると自分のフォームが気になったり,成長記録を残したくなってくるのでこの制限もマイナス要素でした。
24hジムへ入会
上の不満を解決するために,大学や家周辺の24h系ジムを3店舗ほど見学に回りました。月会費はどこも8000円程度で設備に差はほとんどありません。 筋トレは結局継続することが命なので通いやすさを重視し,家から徒歩8分の「Fから始まる某24hジム」に入会しました。よくわからない無料キャンペーンで水素水を契約させられました。なお,大学のジムは年会費制なので24hジムとの併用をしていました。
先に述べた大学のジムでの不満は解消されたのですが,新たな問題が色々出てきました。
1. 結局は夜遅くにジム行きたくないし日曜はゆっくりしたい
開館時間がネックだと最初は感じていましたが,いざいつでも行ける環境になると,さすがに寝る時間周辺の運動は避けたいとか,日曜は家でだらけていたいとか自分の怠惰な部分が出てきました。
2. 設備が貧弱
都内の24h系ジムは小さめのテナントに置かれていることが多く,どこも設備は最低限です。パワーラック,スミスマシン,ケーブルが1台ずつ,マシンは各部位1台ずつ,ダンベルは30kgまでとか。混雑する時間帯に行くと,確実に待ちが発生します(特にフリーウェイト)。自分は基本的にマシンは脚でしか使わないので,この時間はかなり虚無でした。「有酸素マシンいつも空いてるから半分潰してフリーウェイトとかマシン増やせよ」というのが本音です。ただ,24hジムとしてはこういったコアなトレーニーよりは,「とりあえず有酸素でダイエットしたい」みたいなライトユーザーかつボリューム層を取りたいのかなと思ったりもしています。 結局,フリーウェイトやるなら大学行くかぁ...ということが多くなり,24hジムに行く頻度は徐々に落ちていきました。
3.ベンチが自分の体に合わない
これは入ってみなきゃわからないことですが,パワーラックのベンチ台が自分の身体には少し高すぎたようです。ベンチが高すぎると足に力が入らなくなり,挙上重量が落ちます。例えば大学のジムでベンチプレス65kgが挙がった翌週に24hジムに行くと57.5kgで潰れる,みたいなことが起きました。
割に合わないのよ
振り返ってみると24hジムは月に3,4回程度しか使っていませんでした。1回あたり2000円と考えると全く割に合いません。
以上をまとめると,開館時間に制限のあるジムを格安に使える環境にある人の最適解の1つ(局所最適?)は
格安ジムをメインで使い,休館日には公営ジムもしくはビジター利用可能のジムを使う。
ということになると思います。というか,モチベも色々変化してまあ1週間くらいだったら家で腕立て伏せでもやってればいいやくらいの感覚になってしまいました。 あと社会人になったらゴールドジム行きたいなぁという気持ちです。
Visual Studio CodeでLaTeX環境を構築(備忘録)
環境構築で苦労した経験はあまりないですが,唯一イライラしたのがVS CodeにLaTeX環境を入れた時です。備忘録としていろいろまとめます。
なぜVisual Studio Code
VScodeに乗り換えるまではmac OS用の統合環境であるTeX Shopで書いていました。TeX関連では一番有名かつわかりやすいと評判の奥村先生の美文書作成入門のCD ROMでTeX Live(処理系やらTeX Shopが入ったディストリビューション)をインストールしましたが,特に記憶に残っていないので割と簡単に導入できたはずです。
VS Code×LaTeXの機能としては以下が挙げられます。
- 入力支援,
- 複数のコンパイル設定の使い分け
- 文書のアウトライン表示
- マウスを合わせたときの数式や引用のプレビューやパッケージのドキュメントの表示
- synctex連携
特に1.入力支援(スニペットや予測変換)と4.数式,図のコンパイル前のプレビュー,が便利です。


ある程度TeX記法に慣れると決まり切ったコマンドしか使わなくなるので,入力支援で楽をして浮いた時間を生産的活動に使いましょう。
5のsynctex連携というのは,コンパイル後にtex文書の特定箇所からPDFの該当箇所に飛べたり,その逆ができるという機能です。PDFで誤植を発見したときにすぐにtex文書の該当箇所に飛んで修正,とかが使う場面だと思います。
今セメスターは学生実験でレポートを共同編集する必要が出てきて,オンラインLaTeXエディタ overleafを使ったこともあります。挿入する諸々のファイル(図,ソースコードファイル)の更新のたびにアップロードし直す必要がある煩雑さを除けば,VS Code × LaTeXでできるほぼ全ての機能が使えてしまうので割とアリかもしれません。
LaTeXとVS codeをインストール
特にこだわりがないのならTeX Liveをインストールするのがいいと思います。たぶん。 今ローカル環境でLaTeXを使えている人は飛ばしてください。
下記のサイトがわかりやすいのでインストールの詳細は丸投げします。 texwiki.texjp.org
最近いろいろ調整したくなって,フォントの設定をいじったらバグって再インストールする羽目になったので,TeX LiveではなくMac TeXをインストールしました。気付くのが遅かったのですが,MacTeX には「一度インストールすると、完全なアンインストールは難しい」という性質があるらしいです。下記のサイトが詳しいですが,GhostScript バイナリというやつをシステムのディレクトリにばら撒くため,完全に消去し切るのがほぼ不可能だそう。めっちゃ萎えた。
VS Codeの設定
先程紹介したサイトではlatexmkrcというやつを編集しよう,とか言っていますが,僕の場合初めにこれをいじったせいでエラーが出まくっていました。もし同じ状況だったらターミナルから rm .latexmkrcとかで削除しましょう。
下記のサイトを参考にしました。 texwiki.texjp.org
まずVS CodeでLaTeX Workshopというextensionを使えるようにします。 VS codeの左側にあるアクティビティバーから拡張機能をクリックし,検索フィールドに latex と入力すれば関連拡張機能の一覧が示されます。そこから適切な拡張機能をインストールします。(このとき Japanese Language Pack for VS Code を導入するとメニューや各種設定の説明も日本語化できます。)
Ctrl+Comma (Cmd+Comma) で「設定(Settings)」 タブを開きます。「設定の検索」フィールドに適切な用語を入力して必要な設定を絞り込むことができます。代表的な設定はこの画面上で設定できますが,詳細な設定は settings.json に直接書きこみます。画面右上にある「Open Settings (JSON)」をクリックすると,「ユーザー設定(settings.json)」が開きます。初回は{}しか記述されていない画面が開きますので,その{}内に各種設定を書きこみます。
「ユーザー設定(settings.json)」は「既定の設定(defaultSettings.json)」に優先します。「既定の設定」を確認するには,Ctrl+shift+P (Cmd+shift+P)から default を検索すると見つかります。
このJSONファイルの設定が環境構築の大きな壁になっている気がします。そもそもLaTeXに無限に種類があることをここで初めて知ります。
いろいろ血迷った挙句行き着いたものが以下です。結果オーライ。
{ "latex-workshop.chktex.enabled": false, "latex-workshop.latex.recipes": [ { "name": "ptex2pdf*2", "tools": [ "ptex2pdf", "ptex2pdf" ], }, { "name": "ptex2pdf&pbibtex", "tools": [ "ptex2pdf", "pbibtex", "ptex2pdf", "ptex2pdf" ], } ], "latex-workshop.latex.tools": [ { "name": "ptex2pdf", "command": "ptex2pdf", "args": [ "-interaction=nonstopmode", "-l", "-ot", "-kanji=utf8 -synctex=1 -file-line-error", "%DOC%" ] }, { "name": "pbibtex", "command": "pbibtex", "args": [ "-interaction=nonstopmode", "-kanji=utf8", "%DOCFILE%" ] } ], "latex-workshop.view.pdf.viewer": "tab", "editor.wordWrap": "on", "latex-workshop.latex.autoBuild.run": "onFlieChange", "latex-workshop.latex.clean.enabled": true, "latex-workshop.latex.autoClean.run": "onBuilt" }
ビルドはMacの場合はcommand+option+B,Windowsの場合はctrl+alt+bです。左側のTeXタブでもビルド(Build LaTeX project)できます。生成したPDFはこのタブでView LaTeX PDFをクリックすると開けます。
synctexは有効になっているはずなのでコンパイルしたあと,pdfとtexコードを開いた状態で動作確認しましょう。
- pdfの適当な箇所をcommand+クリック(ctrl+クリック)する。→texコードの該当箇所に飛ぶ
- texコードの適当な場所にカーソルを置いて,command+option+J →pdfの該当箇所に飛ぶ
他にもスニペット(入力支援)をカスタマイズしたりもできますが,デフォルトのスニペットをまず覚えておくと便利です。
- SSE+tabキー →section
- BEQ+tabキー →equation環境
- BTA+tabキー →tabular環境
- BAL+tabキー →align環境
- @a+tabキー →
卒論執筆などで大活躍すること間違いなしだと思うので最適な環境構築をしましょう!
Deep Learningの話
前回の記事からかなり間が空きました。
毎日のようにブログを書いている友人が何人かいますが素直に尊敬です。
自分は記録用というか覚書のためにやっている面も多少あるので,投稿は気まぐれです。
今回は最近勉強した「ゼロから作るDeep Learning- Pythonで学ぶディープラーニングの理論と実装 斎藤康毅著」について。
ディープラーニングの入門書としてはかなり有名なものらしく,Amazonレビューを見ても人気の高さが伺えます。言語はすべてPythonです。
機械学習の知識ゼロの僕でも難なく読めたのでたぶん良書です。
著者の日本語にクセがなく,説明も非常に丁寧な印象を受けました。
この本のコンセプトは,外部のライブラリに頼らず(使うのはNumpyやmatplotlibくらい),Python 3によってゼロからディープラーニングを作りながら原理を学ぶということです。ディープラーニングやニューラルネットワークの基礎だけでなく,誤差逆伝播法(back propagation),畳み込みニューラルネットワーク(CNN)なども実装レベルで理解できます。
最後の方には最近のトレンドや応用例もお話として触れられています。ただここはコードを書いたり,とかは全くないので本当にお話程度。
良いところとしては大事なところは何度も繰り返してくれるので,短期記憶よわよわな人でもついてこれるところだと思います。教養レベルの微積分,線型代数の知識とPythonの文法さえわかっていれば,他の前提知識は要りません。
悪いところをあげるとすれば,途中で意味不明なコードが一箇所だけ登場するところです。たいしたことはないですが,ググると「こういうことやで」という記事がすぐに見つかりました。誤植的なものはほぼ本書のホームページに網羅されているので適宜確認するのが良いと思います。
前半の山場でもある手書き数字認識の学習(パラメータの最適化)で,ある処理を10000回計算させるのですが,その章で「数値微分だと時間かかるから後々紹介する誤差逆伝播を先取りして実装してもいいよ」的な記述がありました。
「時間かかるとかいってもせいぜい数分でしょ」
愚直に数値微分で実行したところ,10分経っても終わらず,20分経っても終わらず…
結局25分で中断したところ,88回しか計算できていませんでした!すると10000回の計算が終わるのは47時間…
back propagationで実装すると15秒くらいで終わりました。back propagationすげえ。
6章あたりから手を動かしながら学ぶ感じではなくなるのでちょっと読むのがきつかったですが,大体1日に1章進めたのでトータルで1週間くらいで読み終わりました。
この本には続編があって2冊目が自然言語処理編,3冊目がフレームワーク編となっています。いまのところ自然言語処理にはあまり興味がないので飛ばしてフレームワーク編を読んでいます(1章が終わったくらい)。読み終わったらこれについても書くかもしれません。
この本と並行して読んだ「人工知能は人間を超えるか ディープラーニングの先にあるもの」も理解を深める上で役に立ちましたし,普通に面白かったです(これは一般書なので気楽に読める)。人工知能の定義の話題で航空宇宙の某教授のお名前が登場して「おお」となったりしました。
部屋に出没した蜘蛛を撃退するのに疲れたので今日はここまで。
虫が嫌いすぎる話など
虫を世界から撲滅したい
ただいま札幌に帰省しています。そこで困ったことを一つ。
東京の家だと,自分が王様なので暑い日でも窓を閉め切ってエアコンをフル稼働させるんですが,実家だとそうはいかなくて,窓を開閉することで暑さに対処することを求められます。
でも,めっちゃ虫が入る。
夜寝ようと思って携帯をぽちぽちしていて,耳元に「ブーン」という不快音がすれば,その晩は寝れたもんじゃありません。
この間は耳の中に虫が入ってきてかなり燃えました。
たぶん,網戸の隙間とかから不法侵入しているんだろうと思いますが,本当にありえない。虫にとっても狭苦しい家屋に入って生涯を終えるのは悔しいだろうし,こちらも見つけ次第抹殺するのに神経を使うだけなのでお互い利益がないです。
いまもブンブンと頭上で飛び回っています。(一匹は適切な方法で処理しました。)
ドキュメンタル シーズン8
一昨日くらいにドキュメンタルのシーズン8全話が公開されましたね。
なんだかんだ最新シーズンが公開されたら,公開日に全話見るくらいには好きなのですが,今回はうーんという感じでした。シーズン7が良過ぎただけに残念。こうなると,ザコシはレギュラーにしてもいいと思いました。
あと,攻撃力が弱い芸人を淘汰するためにも,笑わせた回数に比例して体力ポイント的なのを加算すれば良いのかもと思ったりしました。それだとなかなか退場者が出ずにゲームが回らないとかもありそうだけど,試験的にやってみてほしさがあります。
今日は以上。
Pythonでフライトシミュレーションをする 第3回(最終回)
最終回として,飛行経路に飛行機の姿勢を付け加えたいと思います.
完成形はこんな感じです.
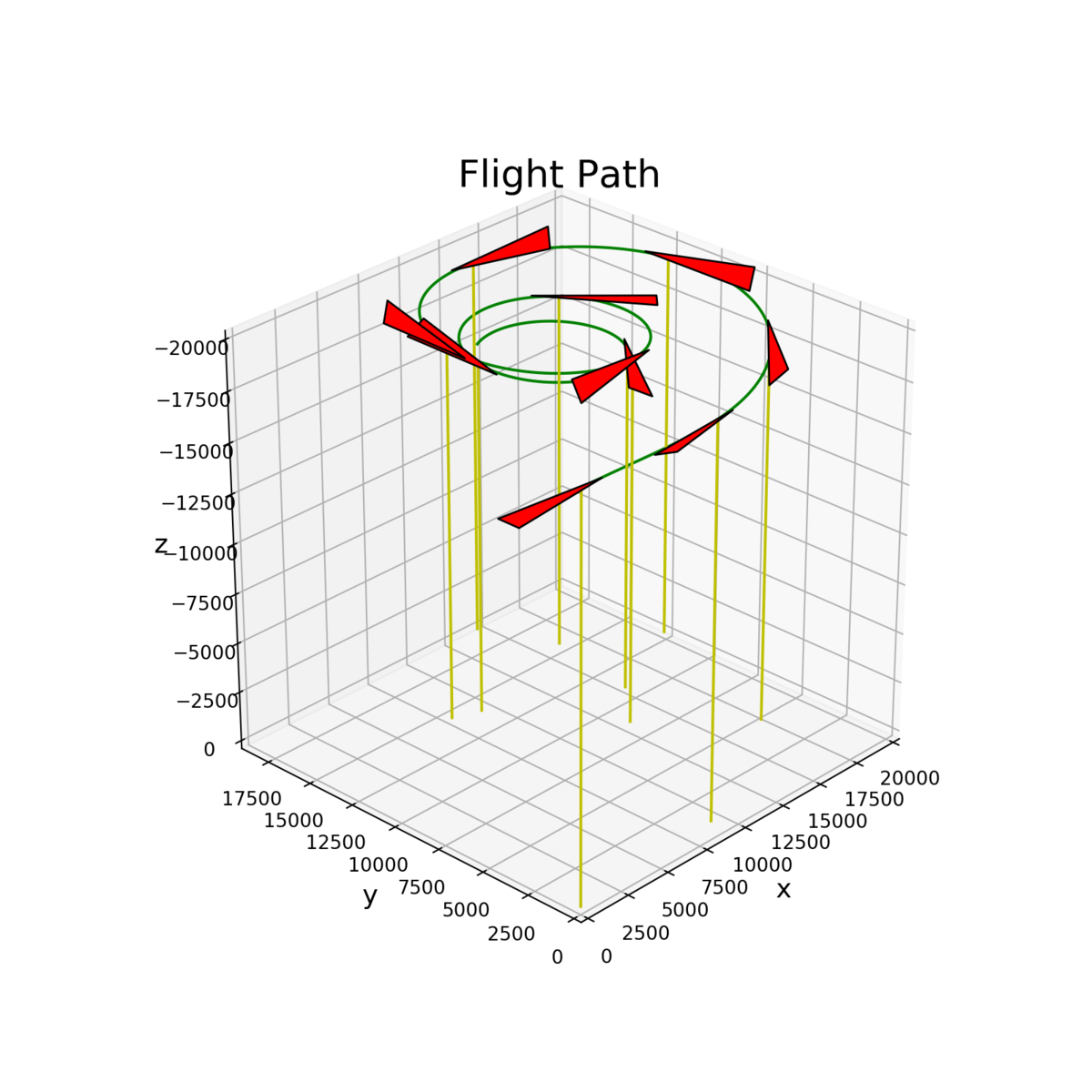
機体固定座標系でxy平面に飛行機っぽい図形を書く.
前回定義した回転写像と,重心位置だけ平行移動させることで地面固定座標系での姿勢に直す.
1と2を適当な時間間隔で繰り返す.
に沿って説明します.
matplotlib 3Dに関しては全くの素人なので,
を参考にしました.
姿勢だけわかればええやん?という思想なので,機体は三角形で勘弁してください.
1. 機体固定座標系でxy平面に飛行機っぽい図形を書く.
art3Dというやつを使えば3Dで線や面を表現できます. 機体は三角形で表現するので,多角形(ポリゴン)を描いてくれるモジュールを使います. 書き方は簡単で以下のように頂点を指定します.
x = [2,-1,-1] y = [0,3,-3] z = [0,0,0]
を結んだ三角形が出来ます.
描画するコードはこんな感じです.
%matplotlib notebook import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D import mpl_toolkits.mplot3d.art3d as art3d #おまじない. fig = plt.figure(figsize=(5,5)) ax = fig.add_subplot(111, projection='3d')#,aspect='equal') #機体の大きさをいじりたければscaleを変える scale=1 #三角形を描く x = [2*scale,-1*scale,-1*scale] y = [0,3*scale,-3*scale] z= [0,0,0] poly = list(zip(x,y,z)) ax.add_collection3d(art3d.Poly3DCollection([poly],color='m')) #軸の範囲を設定 ax.set_xlim(min(x)-1, max(x)+1) ax.set_ylim(min(y)-1, max(y)+1) ax.set_zlim(min(z)-1, max(z)+1) #軸の名前付け ax.set_xlabel("x") ax.set_ylabel("y") ax.set_zlabel("z") plt.show()

2. 前回定義した回転写像と,重心位置だけ平行移動させることで地面固定座標系での姿勢に直す.
1で描いた三角形の頂点は機体固定座標系での座標で表されているので,位置ベクトルと考えましょう.
これを(ある時刻における)回転写像で変換すると,地面固定座標系での機体重心からの位置ベクトルに変換されるので,これに重心位置ベクトルを加えれば座標変換は完了です. これを適当な時間間隔で繰り返せば,イイ感じの図が書けます. (機体の出現頻度や,機体の大きさはその都度調整するしかないと思います.)
まとめ
今までのを全てまとめると以下のようなコードになります.今までの話よくわからんけどとりあえずフライトシミュやってみたいっていう方はコピペしてください笑
import numpy as np import matplotlib.pyplot as plt from math import * from mpl_toolkits.mplot3d import Axes3D import mpl_toolkits.mplot3d.art3d as art3d from mpl_toolkits.mplot3d.art3d import Poly3DCollection #以下,テキストの数値例を写経 #縦の有次元安定微係数 Xu=-0.0215 Zu=-0.227 Mu=0 Xa=14.7 Za=-236 Ma=-3.78 Madot=-0.28 Xq=0 Zq=-5.76 Mq=-0.992 X_deltat=0 Z_deltae=-12.9 Z_deltat=0 M_deltae=-2.48 M_deltat=0 #横の有次元安定微係数 Yb=-45.4 Lb=-1.71 Nb=0.986 Yp=0.716 Lp=-0.962 Np=-0.0632 Yr=2.66 Lr=0.271 Nr=-0.215 Y_deltaa=0 L_deltaa=1.72 N_deltaa=-0.0436 Y_deltar=9.17 L_deltar=0.244 N_deltar=-0.666 #安定軸での水平釣り合い飛行条件での飛行速度などは以下の通り U0=293.8 W0=0 g=9.80 theta0=0.0 #講義プリントの固有運動のところを参考に,4次のルンゲクッタを実行. #x=[u,a,theta,q] 運動変数 #縦の運動パラメータの微分計算 #u1=[delta_e,delta_t] は操縦項 def deriv_pitch(x): du=Xu*x[0]+Xa*x[1]-g*np.cos(theta0)*x[2]-W0*x[3]+X_deltat*u1[1] da=Zu/U0*x[0]+Za/U0*x[1]+(U0+Zq)/U0*x[3]+Z_deltae/U0*u1[0]+Z_deltat/U0*u1[1] dtheta=x[3] dq=(Madot*Zu/U0+Mu)*x[0]+(Ma+Madot*Za/U0)*x[1]-Madot*g*np.sin(theta0)/U0*x[2]+(Madot*(U0+Za)+Mq*U0)/U0*x[3]+(M_deltae+Madot*Z_deltae/U0)*u1[0]+(M_deltat+Madot*Z_deltat/U0)*u1[1] dx=np.array([du,da,dtheta,dq]) return dx #時間の刻み幅 dt=0.1 #時間の計算範囲 Tmax=300 T= np.arange(0.0,Tmax,dt) N = len(T) X = np.zeros((N,4)) #微小擾乱の初期値 u0=0 a0=0 q0=0.01 theta_ini=0 #操縦桿は固定 u1=[0.01,0] #運動変数を格納する行列 X[0,:]=np.array([u0,a0,theta_ini,q0]) for i in range(1,N): k1 = deriv_pitch(X[i-1,:]) k2 = deriv_pitch(X[i-1,:]+0.5*dt*k1) k3 = deriv_pitch(X[i-1,:]+0.5*dt*k2) k4 = deriv_pitch(X[i-1,:]+dt*k3) X[i,:] = X[i-1,:] + dt/6 * (k1+2*k2+2*k3+k4) #横の微分計算 縦と同様 #y(t)=[beta,p,r,phi,psi] #操縦項 u=[delta_a,delta_r] def deriv_yaw(y,u2): dbeta=Yb/U0*y[0]+Yp/U0*y[1]+(Yr/U0-1)*y[2]+g/U0*y[3]+Y_deltar/U0*u2[1] dp=Lb*y[0]+Lp*y[1]+Lr*y[2]+L_deltaa*u2[0]+L_deltar*u2[1] dr=Nb*y[0]+Np*y[1]+Nr*y[2]+N_deltaa*u2[0]+N_deltar*u2[1] dphi=y[1] dpsi=y[2] dy=np.array([dbeta,dp,dr,dphi,dpsi]) return dy Y = np.zeros((N,5)) #微小擾乱の初期値 beta0=0 p0=0 r0=0 phi0=-0.1 psi0=0 #操縦項は定数 操縦桿固定 u2=[0,0] #状態変数を格納する行列 Y[0,:]=np.array([beta0,p0,r0,phi0,psi0]) for i in range(1,N): k1 = deriv_yaw(Y[i-1,:],u2) k2 = deriv_yaw(Y[i-1,:]+0.5*dt*k1,u2) k3 = deriv_yaw(Y[i-1,:]+0.5*dt*k2,u2) k4 = deriv_yaw(Y[i-1,:]+dt*k3,u2) Y[i,:] = Y[i-1,:] + dt/6 * (k1+2*k2+2*k3+k4) #回転写像 def rotation(theta,phi,psi,U,V,W): A=np.array([[np.cos(theta)*np.cos(psi), np.sin(phi)*np.sin(theta)*np.cos(psi)-np.cos(phi)*np.sin(psi), np.cos(phi)*np.sin(theta)*np.cos(psi)+np.sin(phi)*np.sin(psi)], [np.cos(theta)*np.sin(psi), np.sin(phi)*np.sin(theta)*np.sin(psi)+np.cos(phi)*np.cos(psi), np.cos(phi)*np.sin(theta)*np.sin(psi)-np.sin(phi)*np.cos(psi)], [-np.sin(theta), np.sin(phi)*np.cos(theta), np.cos(phi)*np.cos(theta)] ]) velocity=np.array([U,V,W]) return np.dot(A,velocity) #飛行経路を格納する行列 x_e = np.zeros((N,3)) #初期位置は高度1500ftとする x_e[0,:]=np.array([0,0,-3000]) for i in range(1,N): U=U0+X[i-1,0] V=(U0+X[i-1,0])*Y[i-1,0] W=(U0+X[i-1,0])*X[i-1,1] #地面固定座標系での速度dx_e=(x_e,y_e,z_e)を計算 dx_e=rotation(theta0+X[i-1,2],Y[i-1,3],Y[i-1,4],U,V,W) #オイラー法で積分 x_e[i,:]=x_e[i-1,:]+dx_e*dt %matplotlib notebook # Figureを追加 fig = plt.figure(figsize = (8, 8)) # 3DAxesを追加 ax = fig.add_subplot(111, projection='3d') # Axesのタイトルを設定 ax.set_title("Flight Path", size = 20) # 軸ラベルを設定 ax.set_xlabel("x", size = 14) ax.set_ylabel("y", size = 14) ax.set_zlabel("z", size = 14) #add_lineで重心位置を結び,飛行経路を図示する. line= art3d.Line3D(x_e[:,0],x_e[:,1],x_e[:,2], color='g') ax.add_line(line) #ここから機体の図示 #機体の大きさを調整するパラメータ scale=1.5 #機体を出現させる頻度 interval=400 Tb=np.arange(0,N,interval) #飛行機の頂点 形を変えたければここをいじる x_b = [2000*scale,-7000*scale,-7000*scale] y_b = [0,700*scale,-700*scale] z_b= [0,0,0] for i in Tb: #i番目の姿勢角 theta=X[i,2] phi=Y[i,3] psi=Y[i,4] #座標変換した後の機体の座標たちを格納 a=[] b=[] c=[] for j in range(0,3): #回転写像を作用させた後,重心座標を加えて平行移動 v=rotation(theta,phi,psi,x_b[j],y_b[j],z_b[j])+x_e[i,:] a.append(v[0]) b.append(v[1]) c.append(v[2]) #頂点をリストでまとめる poly = list(zip(a,b,c)) #三角形を描く body=art3d.Poly3DCollection([poly],color='r') #三角形のフチを黒くする body.set_edgecolor('k') ax.add_collection3d(body) #重心位置(x,y,z)からz=0平面に垂線を下ろし,高度を可視化する. #要は(x,y,z)と(x,y,0)を直線で結んでいる. line= art3d.Line3D([x_e[i,0],x_e[i,0]],[x_e[i,1],x_e[i,1]],[x_e[i,2],0], color='y') ax.add_line(line) ax.set_xlim(0, max(x_e[:,0])) ax.set_ylim(min(x_e[:,1]),max(x_e[:,1])) ax.set_zlim(0, min(x_e[:,2])) plt.show()
これを実行するとこうなります.

パラメータを変えれば飛び方もいろいろ変わります.慣れると思い通りできると思います.


コツとしては,軸ごとに縮尺が異なると形がバグるので,一回シミュレーションしてみて最大のレンジに合わせればイイ感じに描けると思います.
夏休みも残り1ヶ月か〜結構あっという間に時間が過ぎました. 友人との札幌旅行(地元)も楽しみです.
あと,周りの人が結構Deep Learningをやっているので入門します.
↓優秀な学科同期からお勧めされたので今日買ってきました.
今日は以上です.
Pythonでフライトシミュレーションをする 第2回
前回は縦の運動を扱ったので,その続きとして横の運動を実装します.
そもそも何をやっているかというと,航空機の運動が釣り合い飛行からの微小擾乱であると仮定して,航空機の運動を互いに連成しないピッチ運動(機首上げ下げ)とロール&ヨー運動の2つのグループに分けています.これは線形化の恩恵で,非線形のままだとこれらが互いに連成してしまいます.
前回,短周期モード,フゴイドモードの話を最後にしたので,補足しておくと,航空機の運動は数学的には以下の5つのモードを用いると表現できます.
縦の運動
短周期モード
長周期モード(フゴイドモード)
横の運動
ダッチロールモード
ロールモード
スパイラルモード
古典力学の連成振動の振動モードみたいにこれらの5つのモードを重ね合わせればいかなる運動も表現できるということです(すげえ).最終回でこれらのモードをシミュレーションで確かめるかもです.
パイロットはこの運動モードを熟知していないと,運動や振動を修正しようとしてもかえってこれらの運動を増大させるような操縦をしてしまうことがあって,PIO(Pilot Induced Oscillation)と呼ばれています.実際にPIOが事故につながった例もいくつかあるようです.
1. 線形化された横の運動方程式
縦と同様です.
とおくと,
と記述できます.
2. 実装!
import numpy as np import matplotlib.pyplot as plt from math import * #横の有次元安定微係数 Yb=-45.4 Lb=-1.71 Nb=0.986 Yp=0.716 Lp=-0.962 Np=-0.0632 Yr=2.66 Lr=0.271 Nr=-0.215 Y_deltaa=0 L_deltaa=1.72 N_deltaa=-0.0436 Y_deltar=9.17 L_deltar=0.244 N_deltar=-0.666 #安定軸での水平釣り合い飛行条件での飛行速度などは以下の通り U0=293.8 W0=0 g=9.80 theta0=0.0 #時間の刻み幅 dt=0.1 #時間の計算範囲 Tmax=300 T= np.arange(0.0,Tmax,dt) N = len(T) #横の微分計算 縦と同様 #y(t)=[beta,p,r,phi,psi] #操縦項 u2=[delta_a,delta_r] def deriv_lateral(y,u2): dbeta=Yb/U0*y[0]+Yp/U0*y[1]+(Yr/U0-1)*y[2]+g/U0*y[3]+Y_deltar/U0*u2[1] dp=Lb*y[0]+Lp*y[1]+Lr*y[2]+L_deltaa*u2[0]+L_deltar*u2[1] dr=Nb*y[0]+Np*y[1]+Nr*y[2]+N_deltaa*u2[0]+N_deltar*u2[1] dphi=y[1] dpsi=y[2] dy=np.array([dbeta,dp,dr,dphi,dpsi]) return dy Y = np.zeros((N,5)) #微小擾乱の初期値 beta0=0 p0=0 r0=0 phi0=0 psi0=0 #操縦項は定数 操縦桿固定 u2=[0.01,0] #状態変数を格納する行列 Y[0,:]=np.array([beta0,p0,r0,phi0,psi0]) #4次のルンゲクッタ法 for i in range(1,N): k1 = deriv_lateral(Y[i-1,:],u2) k2 = deriv_lateral(Y[i-1,:]+0.5*dt*k1,u2) k3 = deriv_lateral(Y[i-1,:]+0.5*dt*k2,u2) k4 = deriv_lateral(Y[i-1,:]+dt*k3,u2) Y[i,:] = Y[i-1,:] + dt/6 * (k1+2*k2+2*k3+k4) #グラフ表示 plt.plot(T,Y[:,0]) plt.xlabel('time [s]') plt.ylabel('beta [rad]') plt.grid() plt.show() plt.plot(T,Y[:,1]) plt.xlabel('time [s]') plt.ylabel('p [rad/s]') plt.grid() plt.show() plt.plot(T,Y[:,2]) plt.xlabel('time [s]') plt.ylabel('r [rad/s]') plt.grid() plt.show() plt.plot(T,Y[:,3]) plt.xlabel('time [s]') plt.ylabel('phi [rad]') plt.grid() plt.show() plt.plot(T,Y[:,4]) plt.xlabel('time [s]') plt.ylabel('psi [rad]') plt.grid() plt.show()
これを実行すると,





となり,強そうなグラフが得られます.教科書の解析例とそこまで変わらないので正しくできてそうです.
やっぱり自分で手を動かすと理解も深まるし,イイですね.無限にパラメータ変えて遊んでられます. 高校時代の数学の先生が「自分で作った味噌汁は美味しいので,自分で導出した公式は忘れない」って言ってたのを思い出しました. 自分で書いたコードは美味しい(?)
3. 飛行経路の計算
これまでの計算で機体固定座標系での各時刻における状態量はすべて求まりました. 次に地面固定座標系での飛行経路を計算します.
流れとしては
と言った感じです.線形代数がここで役に立ちます.
詳細な話はテキストを見ていただくことにして先に進みます.
と表されるので,地面固定座標系での速度は
で計算できます.
が成り立つことを利用すると,以下のように飛行経路が計算できます.
import numpy as np import matplotlib.pyplot as plt from math import * from mpl_toolkits.mplot3d import Axes3D #回転写像 def rotation(theta,phi,psi,U,V,W): A=np.array([[np.cos(theta)*np.cos(psi), np.sin(phi)*np.sin(theta)*np.cos(psi)-np.cos(phi)*np.sin(psi), np.cos(phi)*np.sin(theta)*np.cos(psi)+np.sin(phi)*np.sin(psi)], [np.cos(theta)*np.sin(psi), np.sin(phi)*np.sin(theta)*np.sin(psi)+np.cos(phi)*np.cos(psi), np.cos(phi)*np.sin(theta)*np.sin(psi)-np.sin(phi)*np.cos(psi)], [-np.sin(theta), np.sin(phi)*np.cos(theta), np.cos(phi)*np.cos(theta)] ]) velocity=np.array([U,V,W]) return np.dot(A,velocity) #飛行経路を格納する行列 x_e = np.zeros((N,3)) #初期位置は高度1000ftとする x_e[0,:]=np.array([0,0,-1000]) for i in range(1,N): U=U0+X[i-1,0] V=(U0+X[i-1,0])*Y[i-1,0] W=(U0+X[i-1,0])*X[i-1,1] #地面固定座標系での速度dx_e=(x_e,y_e,z_e)を計算 dx_e=rotation(theta0+X[i-1,2],Y[i-1,3],Y[i-1,4],U,V,W) #オイラー法で積分 x_e[i,:]=x_e[i-1,:]+dx_e*dt %matplotlib notebook # Figureを追加 fig = plt.figure(figsize = (8, 8)) # 3DAxesを追加 ax = fig.add_subplot(111, projection='3d') # Axesのタイトルを設定 ax.set_title("Flight Path", size = 20) # 軸ラベルを設定 ax.set_xlabel("x", size = 14) ax.set_ylabel("y", size = 14) ax.set_zlabel("z", size = 14) #データをプロット plt.plot(x_e[:,0],x_e[:,1],x_e[:,2]) ax.set_zlim(-1000,1000) plt.show()
なお,航空機力学の伝統的な座標の取り方ではz軸が鉛直下向きになることに注意します.
(高度1000ftはとなります)

エレベータ角(0.01rad)の定義は機首下げが正なので機体は下降し,エルロン(0.01rad)は右ロールするような方向を正と定めているので図のように右回りにらせんを描きながら下降していきます.(当初これを真逆に勘違いしていたので時間が無限に溶けました...)
次回は飛行機の姿勢も可視化します!

- 作者:知宏, 小高
- 発売日: 2018/01/16
- メディア: 単行本
Pythonでフライトシミュレーションをする 第1回
最近やったことから書いてみようということで,Pythonを用いた航空機の飛行シミュレーションについて書きます.
1.モチベーション
つい数週間前に大学の夏学期が終わり,無為に時間を過ごしていた感が否めなかったので,復習がてら航空機力学,数値計算を扱える題材はないかなと思っていたところ,『航空機力学入門 (加藤寛一郎・大屋昭男・柄沢研治 著 東京大学出版会)』の著者である加藤寛一郎さんの『壊れた尾翼 日航ジャンボ機墜落の真実 (講談社+α文庫)』に出会いました.
1985年の有名な日航機墜落事故について解説する本(かなり本格的)なのですが,その中で出てくる事故機のブラックボックス(コックピットでの会話,飛行機の速度,姿勢などのデータを格納した,車で言うドラレコみたいなやつ)の飛行データによる飛行再現シミュレーションがかなり面白そうでした.
フライトシミュレーション,実装でググったところ,ちょうど「航空機力学入門の実装」みたいな記事
butterfly-effect.hatenablog.com
を見つけたのでやってやろう!と思いました.ただOctaveとかいう数値計算に特化した言語で書かれていて意味不明だったので,Python用に書き直す必要がありました.が,まあ結果的には連立微分方程式をただ脳死で打ち込むだけなので楽でした.
2.必要な方程式
航空機は3次元運動なので重心の運動方程式で3成分,剛体の運動方程式で3成分の計6本で記述されます.なお,以下の方程式は機体固定座標系での記述なので,飛行経路を計算する際に地面固定座標系に直すにはオイラー角の座標変換が必要です(それは追々).
剛体運動方程式はちょっと打ち込むのが怠すぎたのでベクトル表記で省略.
は機体重心周りの角運動量,
は重心周りの空気力,推力などによるモーメントです.詳しくはテキストを参照.
ご覧の通り,未知変数は機体飛行速度,そして角速度
の6個の1階非線形微分方程式です.
このままの形だとさすがに扱いにくいので,線形化をします.
3.線形化された縦の運動方程式
航空機の運動が釣り合い状態からの微小擾乱(例えば)だと仮定して近似します.(どの程度の擾乱まで許されるのかわからない.)
縦の運動
縦の状態量
制御量
とすると,以下のように書けます.
に対し
行列の成分に出てくるとかは有次元安定微係数というやつで機体固有の定数です.
注意が必要なのが安定軸で記述しているので
です. この方程式は線形なので実装しやすい形になりました.
これを4次のルンゲクッタで数値計算させました.(安定微係数は教科書に載っていたロッキードP2V-7機の値です.) Scipyのodeintモジュールを使えば良いのですが,復習のため封印しました.
import numpy as np import matplotlib.pyplot as plt from math import * #以下,テキストの数値例を写経 #縦の有次元安定微係数 Xu=-0.0215 Zu=-0.227 Mu=0 Xa=14.7 Za=-236 Ma=-3.78 Madot=-0.28 Xq=0 Zq=-5.76 Mq=-0.992 X_deltat=0 Z_deltae=-12.9 Z_deltat=0 M_deltae=-2.48 M_deltat=0 #安定軸での水平釣り合い飛行条件での飛行速度などは以下の通り U0=293.8 W0=0 g=9.80 theta0=0.0 #講義プリントの固有運動のところを参考に,4次のルンゲクッタを実行. #x=[u,a,theta,q] 運動変数 #縦の運動パラメータの微分計算 #u1=[delta_e,delta_t] は操縦項 def deriv_pitch(x,u1): du=Xu*x[0]+Xa*x[1]-g*np.cos(theta0)*x[2]-W0*x[3]+X_deltat*u1[1] da=Zu/U0*x[0]+Za/U0*x[1]-g*np.sin(theta0)/U0*x[2]+(U0+Zq)/U0*x[3]+Z_deltae/U0*u1[0]+Z_deltat/U0*u1[1] dtheta=x[3] dq=(Madot*Zu/U0+Mu)*x[0]+(Ma+Madot*Za/U0)*x[1]-Madot*g*np.sin(theta0)/U0*x[2]+(Madot*(U0+Za)+Mq*U0)/U0*x[3]+(M_deltae+Madot*Z_deltae/U0)*u1[0]+(M_deltat+Madot*Z_deltat/U0)*u1[1] dx=np.array([du,da,dtheta,dq]) return dx #時間の刻み幅 dt=0.01 #時間の計算範囲 T= np.arange(0.0,300.0,dt) N = len(T) X = np.zeros((N,4)) #微小擾乱の初期値 u0=0 a0=0 q0=0 theta_ini=0 #操縦項を定数(操縦桿固定) u1=[0.01,0] #運動変数を格納する行列 X[0,:]=np.array([u0,a0,theta_ini,q0]) for i in range(1,N): k1 = deriv_pitch(X[i-1,:],u1) k2 = deriv_pitch(X[i-1,:]+0.5*dt*k1,u1) k3 = deriv_pitch(X[i-1,:]+0.5*dt*k2,u1) k4 = deriv_pitch(X[i-1,:]+dt*k3,u1) X[i,:] = X[i-1,:] + dt/6 * (k1+2*k2+2*k3+k4) plt.plot(T,X[:,0]) plt.xlabel('time [s]') plt.ylabel('u [ft/s]') plt.grid() plt.show() plt.plot(T,X[:,1]) plt.xlabel('time [s]') plt.ylabel('alpha(AoA) [rad]') plt.grid() plt.show() plt.plot(T,X[:,2]) plt.xlabel('time [s]') plt.ylabel('theta [rad]') plt.grid() plt.show() plt.plot(T,X[:,3]) plt.xlabel('time [s]') plt.ylabel('q [rad/s]') plt.grid() plt.show()
操縦項は定数とみなし,操縦桿固定の状況を想定しました.上のコードではエレベータ(昇降舵)を0.01radにしています. これをグラフにすると,こんな感じになります.




ちゃんと短周期モードとフゴイド(長周期)モードが現れているので正しそうです.この例だとフゴイドの周期は70sくらいだとおもいます.
エレベータを使って高度を上げようとすると,x軸方向速度擾乱値uが+6ft/sに収束しているので新たな釣り合い速度299.8ft/sになったことが読み取れます.
※訂正:エレベータ角は機首下げの方向が正なので,高度は下がります.ピッチ角が負になっててずっと疑問でしたが勘違いでした.
思ったんですが,飛行機が高度を上げるときにフワッとなるあの不快な感じって短周期モードのせいなんですかね,どうなんだろう. (1分以上フワッとすることはないし)
いろいろパラメータをいじると挙動が変わって面白いです. 次回は同じように横の運動も書いて,飛行経路を図示したいと思います
![[改訂第8版]LaTeX2ε美文書作成入門 [改訂第8版]LaTeX2ε美文書作成入門](https://m.media-amazon.com/images/I/41IBo5XilPL.jpg)





