Pythonでフライトシミュレーションをする 第3回(最終回)
最終回として,飛行経路に飛行機の姿勢を付け加えたいと思います.
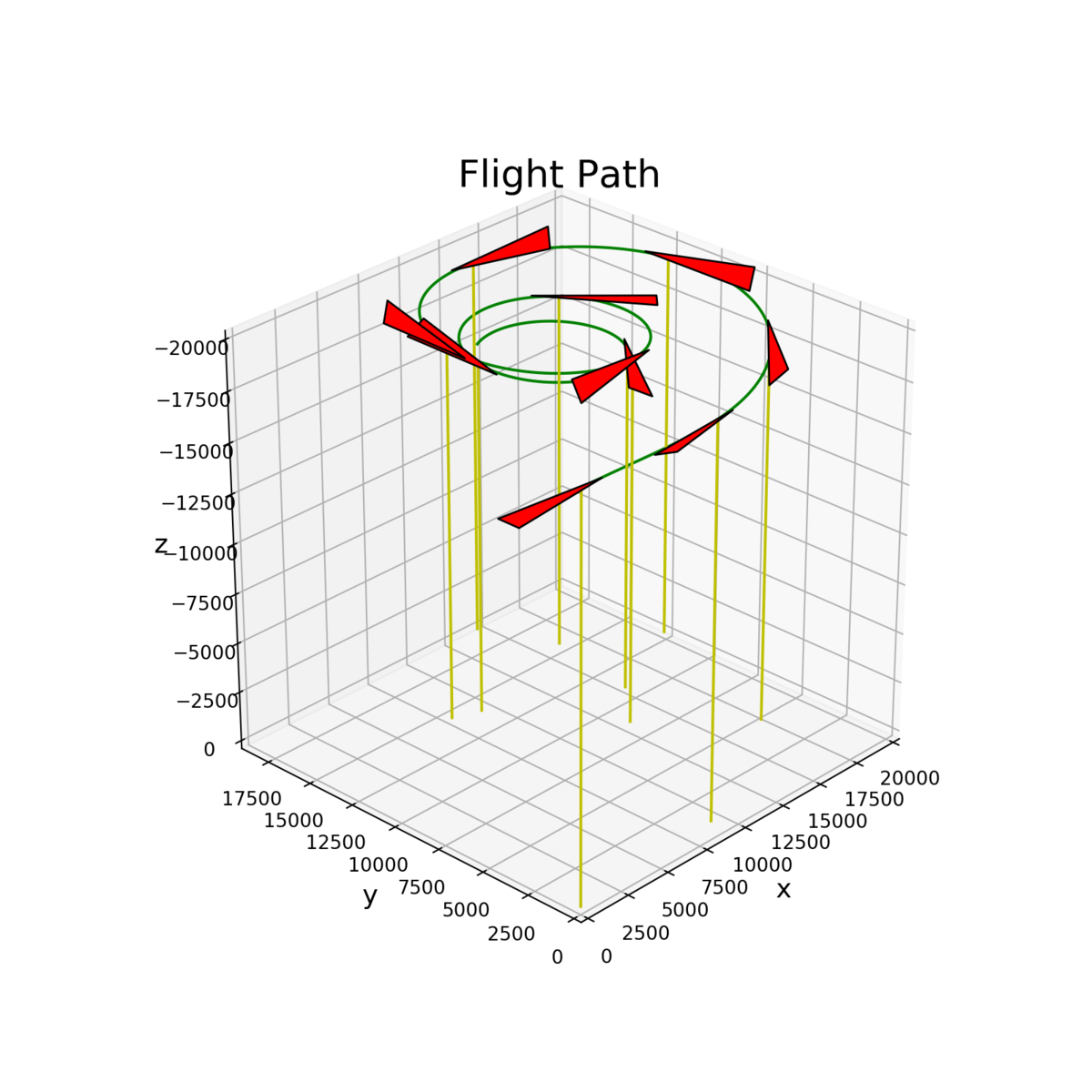
完成形はこんな感じです.
機体固定座標系でxy平面に飛行機っぽい図形を書く.
前回定義した回転写像と,重心位置だけ平行移動させることで地面固定座標系での姿勢に直す.
1と2を適当な時間間隔で繰り返す.
に沿って説明します.
matplotlib 3Dに関しては全くの素人なので,
を参考にしました.
姿勢だけわかればええやん?という思想なので,機体は三角形で勘弁してください.
1. 機体固定座標系でxy平面に飛行機っぽい図形を書く.
art3Dというやつを使えば3Dで線や面を表現できます. 機体は三角形で表現するので,多角形(ポリゴン)を描いてくれるモジュールを使います. 書き方は簡単で以下のように頂点を指定します.
x = [2,-1,-1] y = [0,3,-3] z = [0,0,0]
を結んだ三角形が出来ます.
描画するコードはこんな感じです.
%matplotlib notebook import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D import mpl_toolkits.mplot3d.art3d as art3d #おまじない. fig = plt.figure(figsize=(5,5)) ax = fig.add_subplot(111, projection='3d')#,aspect='equal') #機体の大きさをいじりたければscaleを変える scale=1 #三角形を描く x = [2*scale,-1*scale,-1*scale] y = [0,3*scale,-3*scale] z= [0,0,0] poly = list(zip(x,y,z)) ax.add_collection3d(art3d.Poly3DCollection([poly],color='m')) #軸の範囲を設定 ax.set_xlim(min(x)-1, max(x)+1) ax.set_ylim(min(y)-1, max(y)+1) ax.set_zlim(min(z)-1, max(z)+1) #軸の名前付け ax.set_xlabel("x") ax.set_ylabel("y") ax.set_zlabel("z") plt.show()

2. 前回定義した回転写像と,重心位置だけ平行移動させることで地面固定座標系での姿勢に直す.
1で描いた三角形の頂点は機体固定座標系での座標で表されているので,位置ベクトルと考えましょう.
これを(ある時刻における)回転写像で変換すると,地面固定座標系での機体重心からの位置ベクトルに変換されるので,これに重心位置ベクトルを加えれば座標変換は完了です. これを適当な時間間隔で繰り返せば,イイ感じの図が書けます. (機体の出現頻度や,機体の大きさはその都度調整するしかないと思います.)
まとめ
今までのを全てまとめると以下のようなコードになります.今までの話よくわからんけどとりあえずフライトシミュやってみたいっていう方はコピペしてください笑
import numpy as np import matplotlib.pyplot as plt from math import * from mpl_toolkits.mplot3d import Axes3D import mpl_toolkits.mplot3d.art3d as art3d from mpl_toolkits.mplot3d.art3d import Poly3DCollection #以下,テキストの数値例を写経 #縦の有次元安定微係数 Xu=-0.0215 Zu=-0.227 Mu=0 Xa=14.7 Za=-236 Ma=-3.78 Madot=-0.28 Xq=0 Zq=-5.76 Mq=-0.992 X_deltat=0 Z_deltae=-12.9 Z_deltat=0 M_deltae=-2.48 M_deltat=0 #横の有次元安定微係数 Yb=-45.4 Lb=-1.71 Nb=0.986 Yp=0.716 Lp=-0.962 Np=-0.0632 Yr=2.66 Lr=0.271 Nr=-0.215 Y_deltaa=0 L_deltaa=1.72 N_deltaa=-0.0436 Y_deltar=9.17 L_deltar=0.244 N_deltar=-0.666 #安定軸での水平釣り合い飛行条件での飛行速度などは以下の通り U0=293.8 W0=0 g=9.80 theta0=0.0 #講義プリントの固有運動のところを参考に,4次のルンゲクッタを実行. #x=[u,a,theta,q] 運動変数 #縦の運動パラメータの微分計算 #u1=[delta_e,delta_t] は操縦項 def deriv_pitch(x): du=Xu*x[0]+Xa*x[1]-g*np.cos(theta0)*x[2]-W0*x[3]+X_deltat*u1[1] da=Zu/U0*x[0]+Za/U0*x[1]+(U0+Zq)/U0*x[3]+Z_deltae/U0*u1[0]+Z_deltat/U0*u1[1] dtheta=x[3] dq=(Madot*Zu/U0+Mu)*x[0]+(Ma+Madot*Za/U0)*x[1]-Madot*g*np.sin(theta0)/U0*x[2]+(Madot*(U0+Za)+Mq*U0)/U0*x[3]+(M_deltae+Madot*Z_deltae/U0)*u1[0]+(M_deltat+Madot*Z_deltat/U0)*u1[1] dx=np.array([du,da,dtheta,dq]) return dx #時間の刻み幅 dt=0.1 #時間の計算範囲 Tmax=300 T= np.arange(0.0,Tmax,dt) N = len(T) X = np.zeros((N,4)) #微小擾乱の初期値 u0=0 a0=0 q0=0.01 theta_ini=0 #操縦桿は固定 u1=[0.01,0] #運動変数を格納する行列 X[0,:]=np.array([u0,a0,theta_ini,q0]) for i in range(1,N): k1 = deriv_pitch(X[i-1,:]) k2 = deriv_pitch(X[i-1,:]+0.5*dt*k1) k3 = deriv_pitch(X[i-1,:]+0.5*dt*k2) k4 = deriv_pitch(X[i-1,:]+dt*k3) X[i,:] = X[i-1,:] + dt/6 * (k1+2*k2+2*k3+k4) #横の微分計算 縦と同様 #y(t)=[beta,p,r,phi,psi] #操縦項 u=[delta_a,delta_r] def deriv_yaw(y,u2): dbeta=Yb/U0*y[0]+Yp/U0*y[1]+(Yr/U0-1)*y[2]+g/U0*y[3]+Y_deltar/U0*u2[1] dp=Lb*y[0]+Lp*y[1]+Lr*y[2]+L_deltaa*u2[0]+L_deltar*u2[1] dr=Nb*y[0]+Np*y[1]+Nr*y[2]+N_deltaa*u2[0]+N_deltar*u2[1] dphi=y[1] dpsi=y[2] dy=np.array([dbeta,dp,dr,dphi,dpsi]) return dy Y = np.zeros((N,5)) #微小擾乱の初期値 beta0=0 p0=0 r0=0 phi0=-0.1 psi0=0 #操縦項は定数 操縦桿固定 u2=[0,0] #状態変数を格納する行列 Y[0,:]=np.array([beta0,p0,r0,phi0,psi0]) for i in range(1,N): k1 = deriv_yaw(Y[i-1,:],u2) k2 = deriv_yaw(Y[i-1,:]+0.5*dt*k1,u2) k3 = deriv_yaw(Y[i-1,:]+0.5*dt*k2,u2) k4 = deriv_yaw(Y[i-1,:]+dt*k3,u2) Y[i,:] = Y[i-1,:] + dt/6 * (k1+2*k2+2*k3+k4) #回転写像 def rotation(theta,phi,psi,U,V,W): A=np.array([[np.cos(theta)*np.cos(psi), np.sin(phi)*np.sin(theta)*np.cos(psi)-np.cos(phi)*np.sin(psi), np.cos(phi)*np.sin(theta)*np.cos(psi)+np.sin(phi)*np.sin(psi)], [np.cos(theta)*np.sin(psi), np.sin(phi)*np.sin(theta)*np.sin(psi)+np.cos(phi)*np.cos(psi), np.cos(phi)*np.sin(theta)*np.sin(psi)-np.sin(phi)*np.cos(psi)], [-np.sin(theta), np.sin(phi)*np.cos(theta), np.cos(phi)*np.cos(theta)] ]) velocity=np.array([U,V,W]) return np.dot(A,velocity) #飛行経路を格納する行列 x_e = np.zeros((N,3)) #初期位置は高度1500ftとする x_e[0,:]=np.array([0,0,-3000]) for i in range(1,N): U=U0+X[i-1,0] V=(U0+X[i-1,0])*Y[i-1,0] W=(U0+X[i-1,0])*X[i-1,1] #地面固定座標系での速度dx_e=(x_e,y_e,z_e)を計算 dx_e=rotation(theta0+X[i-1,2],Y[i-1,3],Y[i-1,4],U,V,W) #オイラー法で積分 x_e[i,:]=x_e[i-1,:]+dx_e*dt %matplotlib notebook # Figureを追加 fig = plt.figure(figsize = (8, 8)) # 3DAxesを追加 ax = fig.add_subplot(111, projection='3d') # Axesのタイトルを設定 ax.set_title("Flight Path", size = 20) # 軸ラベルを設定 ax.set_xlabel("x", size = 14) ax.set_ylabel("y", size = 14) ax.set_zlabel("z", size = 14) #add_lineで重心位置を結び,飛行経路を図示する. line= art3d.Line3D(x_e[:,0],x_e[:,1],x_e[:,2], color='g') ax.add_line(line) #ここから機体の図示 #機体の大きさを調整するパラメータ scale=1.5 #機体を出現させる頻度 interval=400 Tb=np.arange(0,N,interval) #飛行機の頂点 形を変えたければここをいじる x_b = [2000*scale,-7000*scale,-7000*scale] y_b = [0,700*scale,-700*scale] z_b= [0,0,0] for i in Tb: #i番目の姿勢角 theta=X[i,2] phi=Y[i,3] psi=Y[i,4] #座標変換した後の機体の座標たちを格納 a=[] b=[] c=[] for j in range(0,3): #回転写像を作用させた後,重心座標を加えて平行移動 v=rotation(theta,phi,psi,x_b[j],y_b[j],z_b[j])+x_e[i,:] a.append(v[0]) b.append(v[1]) c.append(v[2]) #頂点をリストでまとめる poly = list(zip(a,b,c)) #三角形を描く body=art3d.Poly3DCollection([poly],color='r') #三角形のフチを黒くする body.set_edgecolor('k') ax.add_collection3d(body) #重心位置(x,y,z)からz=0平面に垂線を下ろし,高度を可視化する. #要は(x,y,z)と(x,y,0)を直線で結んでいる. line= art3d.Line3D([x_e[i,0],x_e[i,0]],[x_e[i,1],x_e[i,1]],[x_e[i,2],0], color='y') ax.add_line(line) ax.set_xlim(0, max(x_e[:,0])) ax.set_ylim(min(x_e[:,1]),max(x_e[:,1])) ax.set_zlim(0, min(x_e[:,2])) plt.show()
これを実行するとこうなります.

パラメータを変えれば飛び方もいろいろ変わります.慣れると思い通りできると思います.


コツとしては,軸ごとに縮尺が異なると形がバグるので,一回シミュレーションしてみて最大のレンジに合わせればイイ感じに描けると思います.
夏休みも残り1ヶ月か〜結構あっという間に時間が過ぎました. 友人との札幌旅行(地元)も楽しみです.
あと,周りの人が結構Deep Learningをやっているので入門します.
↓優秀な学科同期からお勧めされたので今日買ってきました.
今日は以上です.

